python binary number

We have looked at simple numbers and operations before. In this article you will learn how numbers work inside the computer and a some of magic to go along with that :-)

More detailed: While this is not directly useful in web applications or most desktop applications, it is very useful to know.

In this article you will learn how to use binary numbers in Python, how to convert them to decimals and how to do bitwise operations on them.

Related course:
Python Programming Bootcamp: Go from zero to hero

Binary numbers

At the lowest level, the computer has no notion whatsoever of numbers except ‘there is a signal’ or ‘these is not a signal’. You can think of this as a light switch: Either the switch is on or it is off.

This tiny amount of information, the smallest amount of information that you can store in a computer, is known as a bit. We represent a bit as either low (0) or high (1).

To represent higher numbers than 1, the idea was born to use a sequence of bits. A sequence of eight bits could store much larger numbers, this is called a byte. A sequence consisting of ones and zeroes is known as binary. Our traditional counting system with ten digits is known as decimal.

<caption id=”attachment_824” align=”alignnone” width=”300”] 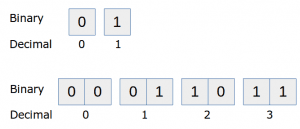Binary numbers and their decimal representation.

Lets see that in practice:

# Prints out a few binary numbers.
print int('00', 2)
print int('01', 2)
print int('10', 2)
print int('11', 2)

The second parameter 2, tells Python we have a number based on 2 elements (1 and 0). To convert a byte (8 bits) to decimal, simple write a combination of eight bits in the first parameter.

# Prints out a few binary numbers.
print int('00000010', 2)   # outputs 2
print int('00000011', 2)   # outputs 3
print int('00010001', 2)   # outputs 17
print int('11111111', 2)   # outputs 255

How does the computer do this? Every digit (from right to left) is multiplied by the power of two.

The number ‘00010001‘ is (1 x 2^0) + (0 x 2^1) + (0 x 2^2) + (0 x 2^3) + (1 x 2^4) + (0 x 2^5) + (0 x 2^6) + (0 x 2^7) = 16 + 1 = 17. Remember, read from right to left.

The number ‘00110010’ would be (0 x 2^0) + (1 x 2^1) + (0 x 2^2) + (0 x 2^3) + (1 x 2^4) + (1 x 2^5) + (0 x 2^6) + (0 x 2^7) = 32+16+2 = 50.

Try the sequence ‘00101010’ yourself to see if you understand and verify with a Python program.

Logical operations with binary numbers

Binary Left Shift and Binary Right Shift
Multiplication by a factor two and division by a factor of two is very easy in binary. We simply shift the bits left or right. We shift left below:

Bit 4	Bit 3	Bit 2	Bit 1
0	1	0	1
1	0	1	0

Before shifting (0,1,0,1) we have the number 5 . After shifting (1,0,1,0) we have the number 10. In python you can use the bitwise left operator (<<) to shift left and the bitwise right operator (>>) to shift right.

inputA = int('0101',2)

print "Before shifting " + str(inputA) + " " + bin(inputA)
print "After shifting in binary: " + bin(inputA << 1)
print "After shifting in decimal: " + str(inputA << 1)

Output:

Before shifting 5 0b101
After shifting in binary: 0b1010
After shifting in decimal: 10

The AND operator

Given two inputs, the computer can do several logic operations with those bits. Let’s take the AND operator. If input A and input B are positive, the output will be positive. We will demonstrate the AND operator graphically, the two left ones are input A and input B, the right circle is the output:

<caption id=”attachment_843” align=”alignnone” width=”640”] Bitwise AND

In code this is as simple as using the & symbol, which represents the Logical AND operator.

# This code will execute a bitwise logical AND. Both inputA and inputB are bits.
inputA = 1
inputB = 1

print inputA & inputB   # Bitwise AND

By changing the inputs you will have the same results as the image above. We can do the AND operator on a sequence:

inputA = int('00100011',2)   # define binary sequence inputA
inputB = int('00101101',2)   # define binary sequence inputB

print bin(inputA & inputB)   # logical AND on inputA and inputB and output in binary

Output:

0b100001   # equals 00100001

This makes sense because if you do the operation by hand:

00100011
00101101
--------   Logical bitwise AND
00100001

The OR operator

Now that you have learned the AND operator, let’s have a look at the OR operator. Given two inputs, the output will be zero only if A and B are both zero.

<caption id=”attachment_847” align=”alignnone” width=”640”] 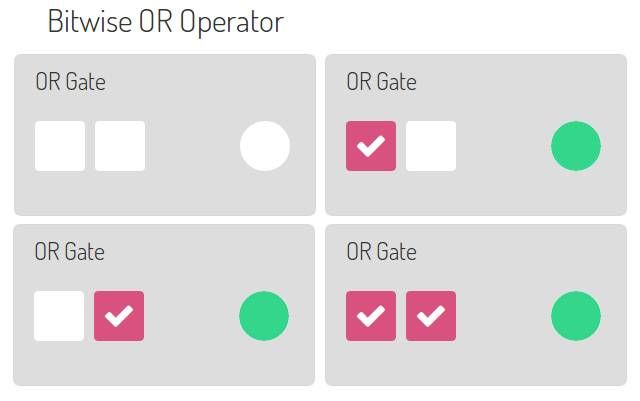binary bitwise OR

To execute it, we use the | operator. A sequence of bits can simply be executed like this:

inputA = int('00100011',2)  # define binary number
inputB = int('00101101',2)  # define binary number

print bin(inputA)            # prints inputA in binary
print bin(inputB)            # prints inputB in binary
print bin(inputA | inputB)   # Execute bitwise logical OR and print result in binary

Output:

0b100011
0b101101
0b101111

The XOR operator

This is an interesting operator: The Exclusive OR or shortly XOR.

<caption id=”attachment_849” align=”alignnone” width=”640”] bitwise XOR

To execute it, we use the ^ operator. A sequence of bits can simply be executed like this:

inputA = int('00100011',2)  # define binary number
inputB = int('00101101',2)  # define binary number

print bin(inputA)            # prints inputA in binary
print bin(inputB)            # prints inputB in binary
print bin(inputA ^ inputB)   # Execute bitwise logical OR and print result in binary

Output:

0b100011
0b101101
0b1110